NSS 4th

发表于 2025-09-05 更新于 2025-09-11 阅读次数：本文字数： 6.1k 阅读时长 ≈ 11 分钟

owo

依旧是赛后复现，主要是锻炼一下cuso的使用

Guillotine

import random

flag = 'NSSCTF{**************************}'
p, n, m = 257, 36, 50
e = [choice(range(-3,4)) for i in range(m)]
secret = random.randrange(1,2^n)

random.seed(int(1337))
A = [[[random.randrange(p) for i in range(2)] for j in range(n)] for i in range(m)]
B = []

for time in range(m):
    b = (sum(A[time][j][(secret >> j) & 1] for j in range(n))+e[time])%p
    B.append(b)

print("give you B:",B)

alarm(10)
print("The time for defiance is over. Provide the encryption key, and you shall be granted the mercy of a swift end. Refuse, and your death will be prolonged.")
assert int(input(">")) == secret
print(f"Do you really think I would let you go? {flag}")

题目大意是给出了A,B，并且e∈(-3,3),并且我们一共有50组式子

1	b = (sum(A[time][j][(secret >> j) & 1] for j in range(n))+e[time])%p

提一嘴这里的(secret >> j) & 1指的就是secret的第j位(先把第j位挪到最右边，然后保留最后一位，其他位全部清零)，然后我们根据这个比特选择 A[time][j][0] 或A[time][j][1]。对于这个选择我们仍然可以用数学式子来表示。

假设 x[j]∈{0,1}，即 secret 的第 j 位。
那么：
- 如果 x[j]=0：
  
  At[j][0]⋅(1−0)+At[j][1]⋅0=At[j][0]
- 如果 x[j]=1x[j] = 1x[j]=1：
  
  At[j][0]⋅(1−1)+At[j][1]⋅1=At[j][1]

所以这一项等价于：

At[j][(x[j])

然后我们就可以cuso一把梭(笑)，大致讲一下cuso的用法，就是利用relations，bounds，modulus这三个已知量就能求对应的smallroots了

from pwn import *
import cuso
import random
import os
io = process(['python gui.py'], shell=True)
p = 257
n = 36
m = 50
random.seed(int(1337))

A = [[[random.randrange(p) for i in range(2)] for j in range(n)] for i in range(m)]
line = io.recvline()
parts = line.split(b': ', 1)
if len(parts) < 2:
    raise ValueError(f"无法解析 B 数据，收到: {line!r}")
B = eval(parts[1].decode().strip())
vars = var(','.join([f'x{i}' for i in range(n)]))
es = var(','.join([f'e{i}' for i in range(m)]))
bounds = {vars[i]: (-1, 2) for i in range(n)}
bounds.update({es[i]: (-4, 5) for i in range(m)})
relations = []
for time in range(m):
    equation = sum(A[time][j][0] * (1 - vars[j]) + A[time][j][1] * vars[j] for j in range(n)) + es[time] - B[time]
    relations.append(equation)
roots = cuso.find_small_roots(relations, bounds, modulus=p)[0]
res = ''.join([str(roots[eval(f'x{_}')]) for _ in range(n)])[::-1]
secret = int(res, 2)
print("computed secret:", secret)

io.sendlineafter(b'>', str(secret).encode())
flag = io.recvline()
print(flag)
io.interactive()

LeetSpe4k

from functools import reduce
from random import choice
from secret import flag

le4t = lambda x: "".join(choice(next((j for j in ['a@4A', 'b8B', 'cC', 'dD', 'e3E', 'fF', 'g9G', 'hH', 'iI', 'jJ', 'kK', 'l1L', 'mM', 'nN', 'o0O', 'pP', 'qQ', 'rR', 's$5S', 't7T', 'uU', 'vV', 'wW', 'xX', 'yY', 'z2Z'] if i in j), i)) for i in x.decode())
h4sH = lambda x: reduce(lambda acc, i: ((acc * (2**255+95)) % 2**256) + i, x, 0)

print(le4t(flag), h4sH(flag))
#nSsCtf{H@pPy_A7h_4nNiv3R$arY_ns$C7F_@nD_l3t$_d0_7h3_LllE3t$pEAk!} 9114319649335272435156391225321827082199770146054215376559826851511551461403

很有鸡块风格的代码。

看到h4sH就想到可能是fnv的题，这类题在去年ciscn，今年miniL和d3CTF好像都出现过。

那么直接就有这个式子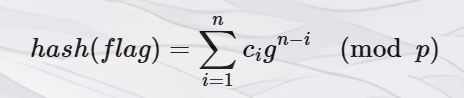

不过这里涉及到一个小技巧，学习了N1gh7ma12e师傅的博客[NSS 4th | N1gh7ma12e的小站](http://n1gh7ma12e.cn/2025/08/25/NSS 4th/)我们需要将“选择”看作一个式子。

比如把a替换成@可以写成(0,1,0,0)$*$(a,@,4,A)$^{T}$

这次咱就不用老办法，来试试科技，继续尝试cuso一把梭

import cuso
from functools import reduce

TABLE = [
    'a@4A', 'b8B', 'cC', 'dD', 'e3E', 'fF', 'g9G', 'hH', 'iI', 'jJ',
    'kK', 'l1L', 'mM', 'nN', 'o0O', 'pP', 'qQ', 'rR', 's$5S', 't7T',
    'uU', 'vV', 'wW', 'xX', 'yY', 'z2Z'
]

h4sH = lambda x: reduce(lambda acc, i: ((acc * (2**255 + 95)) % 2**256) + i, x, 0)

leet_flag = '{H@pPy_A7h_4nNiv3R$arY_ns$C7F_@nD_l3t$_d0_7h3_LllE3t$pEAk!}'

g = 2**255 + 95
p = 2**256

flag_example = 'NSSCTF' + ''.join(
    [c if c in {'{', '}', '_', '!'} else '\x00' for c in leet_flag]
)
flag_example = flag_example.encode()

target_hash = 9114319649335272435156391225321827082199770146054215376559826851511551461403
target_hash -= h4sH(flag_example)

var_groups = []
leet_index = []

pos = -1
for c in leet_flag:
    if c in {'{', '}', '_', '!'}:
        continue
    pos += 1
    for group in TABLE:
        if c in group:
            group_vars = var([f"x_{pos}_{j}" for j in range(len(group))])
            var_groups.append(group_vars)
            leet_index.append(TABLE.index(group))
            break

equations = []
bit_equations = []
bounds = {}

pos = -1
for i, b in enumerate(flag_example):
    if b:
        continue
    pos += 1
    group = TABLE[leet_index[pos]]
    group_vars = var_groups[pos]
    s = sum(group_vars[j] * ord(group[j]) for j in range(len(group)))
    weight = pow(g, len(flag_example) - i - 1, p)
    equations.append(s * weight)
    bit_equations.append(sum(group_vars) - 1)
    for v in group_vars:
        bounds[v] = (-1, 2)

main_equation = sum(equations) - target_hash
relations = [main_equation] + bit_equations

solution = cuso.find_small_roots(relations, bounds=bounds, modulus=p)[0]

flag = ""
pos = -1
for b in flag_example:
    if b:
        flag += chr(b)
        continue
    pos += 1
    group = TABLE[leet_index[pos]]
    group_vars = var_groups[pos]
    for j, v in enumerate(group_vars):
        if solution[v] == 1:
            flag += group[j]
            break

print(flag)

还是大概解释一下这个脚本

var_groups = []
leet_index = []

pos = -1
for c in leet_flag:
    if c in {'{', '}', '_', '!'}:
        continue
    pos += 1
    for group in TABLE:
        if c in group:
            group_vars = var([f"x_{pos}_{j}" for j in range(len(group))])
            var_groups.append(group_vars)
            leet_index.append(TABLE.index(group))
            break

这一段的作用是构造方程的约束。

遍历 flag 模板里的字符：

如果是 { } _ !，跳过（因为这些确定了）。
否则，找到它在 table 里的对应分组，比如 'a@4A'。
给这个字符创建一组 0/1 变量，如 x_5_0, x_5_1, x_5_2, x_5_3，代表在 'a@4A' 里选哪一个。
这些变量保证最终只会选一个候选字符

然后直接构造方程。最后通过解出来的一组变量赋值，找到哪个变量为1，从对应的table里选取字符，拼接得到完整的flag。

HiddenOracle

咕咕