NepCTF2025

发表于 更新于 阅读次数： 本文字数： 19k 阅读时长 ≈ 35 分钟

QAQ

久违的更新，放假后杂七杂八的事情蛮多一直拖到现在

Nepsign

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
from gmssl import sm3
from random import SystemRandom
from ast import literal_eval
from secret import flag

def SM3(data):
    d = [i for i in data]
    h = sm3.sm3_hash(d)
    return h
def SM3_n(data, n=1, bits=256):s
    for _ in range(n):
        data = bytes.fromhex(SM3(data))
    return data.hex()[:bits // 4]


class Nepsign():
    def __init__(self):
        self.n = 256
        self.hex_symbols = '0123456789abcdef'
        self.keygen()

    def keygen(self):
        rng = SystemRandom()
        self.sk = [rng.randbytes(32) for _ in range(48)]
        self.pk = [SM3_n(self.sk[_], 255, self.n) for _ in range(48)]
        return self.sk, self.pk

    def sign(self, msg, sk=None):
        sk = sk if sk else self.sk
        m = SM3(msg)
        m_bin = bin(int(m, 16))[2:].zfill(256)
        a = [int(m_bin[8 * i: 8 * i + 8], 2) for i in range(self.n // 8)]
        step = [0] * 48;
        qq = [0] * 48
        for i in range(32):
            step[i] = a[i]
            qq[i] = SM3_n(sk[i], step[i])
        sum = [0] * 16
        for i in range(16):
            sum[i] = 0
            for j in range(1, 65):
                if m[j - 1] == self.hex_symbols[i]:
                    sum[i] += j
            step[i + 32] = sum[i] % 255
            qq[i + 32] = SM3_n(sk[i + 32], step[i + 32])
        return [i for i in qq]

    def verify(self, msg, qq, pk=None):
        qq = [bytes.fromhex(i) for i in qq]
        pk = pk if pk else self.pk
        m = SM3(msg)
        m_bin = bin(int(m, 16))[2:].zfill(256)
        a = [int(m_bin[8 * i: 8 * i + 8], 2) for i in range(self.n // 8)]
        step = [0] * 48;
        pk_ = [0] * 48
        for i in range(32):
            step[i] = a[i]
            pk_[i] = SM3_n(qq[i], 255 - step[i])
        sum = [0] * 16
        for i in range(16):
            sum[i] = 0
            for j in range(1, 65):
                if m[j - 1] == self.hex_symbols[i]:
                    sum[i] += j
            step[i + 32] = sum[i] % 255
            pk_[i + 32] = SM3_n(qq[i + 32], 255 - step[i + 32])
        return True if pk_ == pk else False


print('initializing...')
Sign = Nepsign()
while 1:
    match int(input('> ')):
        case 1:
            msg = bytes.fromhex(input('msg: '))
            if msg != b'happy for NepCTF 2025':
                print(Sign.sign(msg))
            else:
                print("You can't do that")
        case 2:
            qq = literal_eval(input('give me a qq: '))
            if Sign.verify(b'happy for NepCTF 2025', qq):
                print(flag)

唉被ai打爆的一题。

分析代码不难看出是一个基于哈希链上的签名，我们可以通过任意次输入明文得到对应签名，要求给出规定明文的签名来得到flag。

这道题的攻击方式基于哈希链的一个特点-“可追赶”性质。

由于哈希链是顺序累积的，有如下性质：

1
SM3_n(SM3_n(sk[i], s), t) = SM3_n(sk[i], s + t)

已知sigma_obs[i] = SM3_n(sk[i], MIN_STEP[i])，想得到SM3_n(sk[i], target_step[i])，只需再做target_step[i] - MIN_STEP[i]次哈希

1
2
3
4
5
SM3_n(sigma_obs[i], target_step[i] - MIN_STEP[i])
= SM3_n(SM3_n(sk[i], MIN_STEP[i]), target_step[i] - MIN_STEP[i])
= SM3_n(sk[i], MIN_STEP[i] + (target_step[i] - MIN_STEP[i]))
= SM3_n(sk[i], target_step[i])
= sigma_target[i]

所以思路就很清晰了，我们输入随机生成的32字节的消息。然后得到对应签名。通过签名函数中计算step的部分计算该消息的step。这里我们把它单独提出来

1
2
3
4
5
6
7
8
9
10
11
12
def steps_from_msg(msg: bytes):
    h = SM3(msg)
    m_bin = bin(int(h, 16))[2:].zfill(256)
    a = [int(m_bin[8 * i:8 * i + 8], 2) for i in range(32)]
    step = a + [0] * 16
    for i in range(16):
        s = 0
        for j, ch in enumerate(h, 1):
            if ch == HEX[i]:
                s += j
        step[32 + i] = s % 255
    return step

检查每个分量，如果这次新采集到的步数比历史最小步数还小，则更新最小步数和签名。如果所有分量的最小步数都≤目标消息的step[i]。因为只有拥有比目标步数小的签名，才能通过继续哈希“追赶”到目标步数。然后根据之前讲到的性质对每个分量进行(target_step[i] - MIN_STEP[i])次SM3哈希即可。(也可以利用相同位置产生相同签名来进行碰撞)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
from gmssl import sm3
from os import urandom
from pwn import remote, context

context.log_level = 'warning'
HOST, PORT = 'nepctf30-yb67-wgkm-f37g-75ppqjxnr857.nepctf.com', 443

target_msg = b'happy for NepCTF 2025'
HEX = '0123456789abcdef'
def SM3(data: bytes) -> str:
    return sm3.sm3_hash(list(data))
def steps_from_msg(msg: bytes):
    h = SM3(msg)
    m_bin = bin(int(h, 16))[2:].zfill(256)
    a = [int(m_bin[8 * i:8 * i + 8], 2) for i in range(32)]
    step = a + [0] * 16
    for i in range(16):
        s = 0
        for j, ch in enumerate(h, 1):
            if ch == HEX[i]:
                s += j
        step[32 + i] = s % 255
    return step


target_step = steps_from_msg(target_msg)


def sm3_n(hexstr, n):
    d = bytes.fromhex(hexstr)
    for _ in range(n):
        d = bytes.fromhex(SM3(d))
    return d.hex()



MIN_STEP = [999] * 48
SIGMA = [''] * 48

io = remote(HOST, PORT,ssl=True)
io.recvuntil(b'initializing...')

while True:
    # 随机消息
    m = urandom(32)
    io.sendlineafter(b'> ', b'1')
    io.sendlineafter(b'msg: ', m.hex().encode())
    raw = io.recvline().strip()
    print(raw)
    sig = eval(raw.decode())
    step_obs = steps_from_msg(m)

    updated = False
    for i in range(48):
        if step_obs[i] < MIN_STEP[i]:
            MIN_STEP[i] = step_obs[i]
            SIGMA[i] = sig[i]
            updated = True
    if all(MIN_STEP[i] <= target_step[i] for i in range(48)):
        break

print('[+] coverage OK, forging...')

sigma_final = [
    sm3_n(SIGMA[i], target_step[i] - MIN_STEP[i])
    for i in range(48)
]

io.sendlineafter(b'> ', b'2')
io.sendlineafter(b'give me a qq: ', str(sigma_final).encode())
print(io.recvline().decode().strip())
io.close()

ezRSA2

好耶，随缘师傅的题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from Crypto.Util.number import getStrongPrime, getRandomNBitInteger, GCD, inverse, long_to_bytes, bytes_to_long, sieve_base  
from flag import flag  
  
def gen_parameters(gamma=0.33, beta=0.33):  
    p = getStrongPrime(1024)  
    q = getStrongPrime(1024)  
    N = p*q  
    phi = (p-1)*(q-1)  
    while True:  
        d = getRandomNBitInteger(int(2048*beta))  
        if GCD(d, phi) == 1:  
            break  
    e = inverse(d, phi)  
      
    hints = []  
    M = 1  
    for i in range(1, len(sieve_base)):  
        li = sieve_base[i]  
        hints.append(d%li)  
        M *= li  
        if M.bit_length() >= 1024*gamma:  
            break  
    return e, N, hints  
  
  
  
def main():  
    e,N,hints = gen_parameters()  
    print(f'e={hex(e)}')  
    print(f'N={hex(N)}\n')  
    print(f'hints={hints}\n')  
      
    flag_prefix = b'NepCTF{'  
    assert flag.startswith(flag_prefix)  
    assert flag.endswith(b'}')  
      
    pt = bytes_to_long(flag[len(flag_prefix):-1])  
    ct = pow(pt, e, N)  
    print(f'ct={hex(ct)}')  
      
main()  
  
  
"""
e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29
N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e
"""

当时第一想法也是直接造格做，看了随缘师傅的wp才知道打二元copper也可行，两种方法都写一下吧。当然首先crt求出部分d还是不变的

根据

1
2
3
4
5
6
7
8
hints = []  
    M = 1  
    for i in range(1, len(sieve_base)):  
        li = sieve_base[i]  
        hints.append(d%li)  
        M *= li  
        if M.bit_length() >= 1024*gamma:  
            break

就能得到d的低位

1
dl = CRT(hints, list(sieve_base)[1:len(hints)+1])

格

我们设

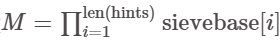
Ofkbvc.png

并令r=p+q

根据RSA可以列出等式$ed-1=k(N-r+1)$将d换为$dl+k_1M$，这里可以列出$e(dl+k_1M)-1=k_2(N-r+1)$然后展开移项$e\cdot dl-1+k_1e\cdot M+k_2(N+1)=k_2r$。那么我们就可以根据这个等式造格
$$
(k_1,1,k_2) \left(\begin{matrix} 1&&e\cdot tmp\ &1&e\cdot dl-1\ &&N+1\ \end{matrix}\right) =(k_1,1,k_2r)
$$
因为d=dl+k$_1$M,所以我们可以大致估计k1和k2的数量级分别为2$^{333}$和2$^{673}$,那么我们肯定要乘上大数进行配平，根据k_2r的数量级来判断下，分别乘一个2$^{1365}$和2$^{1698}$,然后直接造格打即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from Crypto.Util.number import *

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29
N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

hints = [1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]
d0 = CRT(hints, list(sieve_base)[1:len(hints)+1])
M = prod(list(sieve_base)[1:len(hints)+1])
print(dd)
Ge = Matrix(ZZ, 3, 3)
Ge[0, 0] = 2 ** 1365
Ge[1, 1] = 2 ** 1698
Ge[0, 2] = e*M
Ge[1, 2] = e*d0-1
Ge[2, 2] = N+1

L = Ge.LLL()

for row in L:
    d = dd + row[0]//K1*tmp
    print(int(d).bit_length(), row[1]==K2)
    if int(d).bit_length() == int(2048*0.33):
        m = pow(ct, d, N)
        print(long_to_bytes(int(m)))


二元copper

还是根据$e(dl+k_1M)-1=k_2(N-r+1)$这个式子，等式两边同时模eM，得到$1-edl+k(N+1-r)=0 mod eM$，直接对K和r打二元copper即可

(搬一手随缘师傅的脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
from Crypto.Util.number import sieve_base, long_to_bytes
import itertools
from sage.all import *
import time

beta = 0.33

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29
N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

# defund small_roots
# https://github.com/defund/coppersmith
def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    if isinstance(f, Polynomial):
        x, = polygens(f.base_ring(), f.variable_name(), 1)
        f = f(x)

    R = f.base_ring()
    N = R.cardinality()
    
    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)

    G = Sequence([], f.parent())
    for i in range(m+1):
        base = N**(m-i) * f**i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)
    st1 = time.time()
    
    B = (B.dense_matrix()).LLL(epsilon=0.99)
    # B = flatter(B)
    
    end = time.time()
    print(f'time of lattice reduction: {end-st1}s')
    print(f'{B.dimensions() = }')
    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1/factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B*monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []

li_list = list(sieve_base[1:len(hints)+1])

def attack():
    M = prod(li_list)
    print(f'{M.bit_length() = }')
    dM = CRT(hints, li_list)
    # ed-1 = k(N+1-(p+q))
    # k(N+1)-k(p+q)-(e*dM-1) = 0(eM)
    print(f'{dM = }')
    print(f'{dM.bit_length() = }')

    PR = PolynomialRing(Zmod(e*M), 'x,y')
    x,y = PR.gens()

    f = x*(N+1)-x*y-(e*dM-1)

    XX = (e*2**ceil(2048*beta)) // N
    YY = 3*2**1024

    roots = list(small_roots(f, [XX,YY], m=1))
    print(roots)
    assert len(roots) == 1

    k, r = roots[0]
    # ed-1=k(N+1-r)
    k, r = ZZ(k), ZZ(r)
    d = (k*(N+1-r) + 1) // e
    
    print(f'{d=}')
    print(f'{d.bit_length() = }')
    assert e*d-1==k*(N+1-r)

    pt = pow(ct, d, N)
    print(long_to_bytes(pt))
    
def main():
    attack()
    
main()

Lattice Bros

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#已知α的极小多项式为三次多项式f(x),即f(α)=0,且α≈54236.606188881754809671280151541781895183337725393
#上述极小多项式的常数项为a0

from secret import a0,alpha
import gmpy2
from Crypto.Util.number import long_to_bytes
import random
from math import sqrt,log2

d=981020902672546902438782010902608140583199504862558032616415
p = d - a0

k=sqrt(log2(p))+log2(log2(p))
B = 2**30
assert B < p/2**k

m = 30
assert m > 2*sqrt(log2(p))

samples = []
betas = []

f = open("samples.txt",'w')
for _ in range(m):
    t = random.randint(1, p-1)
    beta = random.randint(-B + 1, B - 1)
    a = (t * alpha - beta) % p
    samples.append((t, a))
    betas.append(beta)

f.write(str(samples))

for i in range(0,30):
    assert (betas[i]-samples[i][0]*alpha+samples[i][1])%p == 0

#flag = long_to_bytes(alpha)

首先我们要恢复极小多项式的常数项，参考A Gentle Tutorial for Lattice-Based Cryptanalysis的3.6可以知道我们可以造如下格(截个原文的图，实际应该把8换成45，这与给出的精度有关)

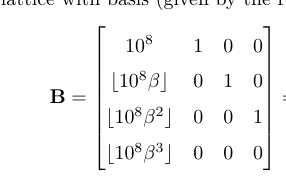
OfkWUq.png

直接规约就能得到目标向量啦。后来看Swizzer师傅的博客，才了解到sage有内置的函数直接求极小多项式Miscellaneous arithmetic functions - Standard Commutative Rings

恢复了之后这就是一个HNP问题了。

OfkFNG.png

因为这里式子里是减法，所以r那一行的负号也就没必要加了。不过因为配平的原因，尝试发现多乘一个4能规约出结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
a = RealField(200)(54236.606188881754809671280151541781895183337725393)
N = 10^45
L = matrix(ZZ, [[floor(N), 1, 0, 0],
                [floor(N * a), 0, 1, 0],
                [floor(N * a**2), 0, 0, 1],
                [floor(N * a**3), 0, 0, 0]])
res = L.LLL()[0]
a0 = res[1]
print(a0)
samples = [(541847931463604073209188621415697353813245102261880389530448, 293760933113243563398917466885108625646262447370201484418246), (235213326900086489464935804156966465366154623411555613791270, 660823982268225103178763707015491421784294988488272636270997), (826464884761457937459245903152143755707241416981488127320435, 428521663319038461250005113612781686761766888058391496085911), (589542000504317435156560078533519448295689695687499354390208, 155284353896000150766154807679279597476176668344402166959399), (968823371588600973965757332601758200815345862153455338808286, 870008943690791009196027169525956126827736285614393106689402), (621636099728440147413990266662022925118216803638588918660041, 265635912066749696542909843111997941904342442664219734956888), (426696569424050102229606043215592727790577655338668728275370, 279313121876980354011480010042682666651614765507190502627689), (89450479064580125731654556963306718472532905610952012502649, 465933125964565419295325650759566635253450915499965633327941), (480355476500393865742379469913983270769356894135485925662119, 894041172171871806404285309781862268351135623868845025443422), (842436524669577199024236805258573090764419350786291073287889, 345478552143958037534551648319293899442551000874041707820740), (650054674429185550652935714084022116516082323269321462104664, 441999979283903658157822753439653947343822546158589507765994), (46289431385578693366971976442426853079852982529357847290686, 625618376463384339878849844467050454204685252824782609369180), (71444185449163133531919043374545893927347050624346741281881, 955925578289311966288639224625142299309823207245807788495453), (192579726169321656812883068526498248523814846320328766176253, 626481822474054336470183912297952839011392733501646931370367), (736527635648804640774976580747540045854351230084566721853611, 276626211757586963928788091386096607703513204646314683038338), (177922521867185878959621840269164617147915792720210315529733, 541058782621716573816245900423919799500476442285991532228641), (40610451174818168154306630612571678739921107216052349044576, 727642592899858828601137105077611015328512898368636299587376), (385012983728389322601149562441674995471397288632464238356283, 353921151307105661267278594470212933060655245893209524497156), (750447975601038834764379841158092390933760641866111445401426, 391626416964965737035878375834907580903143512300198923948189), (115058604943298010958881205548782439407592353731185670266593, 491630592857258949793489206081490523001249620510479961058022), (327389234395954477946639629629085910688793716425320663599360, 24975272330009592102362429346350824580378490147041708568130), (115595274689129534885608766476695918464309130165432995990883, 757961876891952019297626599379744405302595090402128271144165), (950804723308776351161744501221236453742418549093165078282534, 20307246759635231945223392614290397512873344480184942904518), (724537610412063699714461780160573528810830178440136810747811, 149681928388378582933943374524511804362928290938917573644613), (340891278018589324130004945217960336392205386747747011263373, 683307718413135477104477081812052183267507312278283317237187), (104379682905784169840335131193505192063050242530811180817410, 715010230598797717533306270232399781090458356371977748416491), (644160326926600986730919713173510327120201404569141824224075, 127877985489410167008195578625004740882394608402141169695352), (549253388716005399852261816416312267100135940382820676807345, 210560134643237517255193955173709174155305784935427470113433), (968265711632086435506163736279856957220961064226797549228006, 273174723915971720522674140326199419265943707917542063022561), (704367622558261900937184683100177434487519780290678439135652, 959106497548134540301589019840013331842784496835379005298630)]

n = 30
d = 981020902672546902438782010902608140583199504862558032616415
B = 2**30
p = d - a0
print(p)
rs = []
cs = []
for r_val, t_val in samples:
    rs.append(r_val)
    cs.append(t_val)
t = len(rs)
P = identity_matrix(t) * p
RC = matrix([[-r for r in rs], cs])
KP = matrix([[B*4 / p, 0], [0, B]])
M = block_matrix([[P, 0], [RC, KP]], subdivide=False)
shortest_vector = M.LLL()
assert shortest_vector == re
x = int(abs(shortest_vector[1][-2] * p)) // (B * 4)
print(long_to_bytes(x))