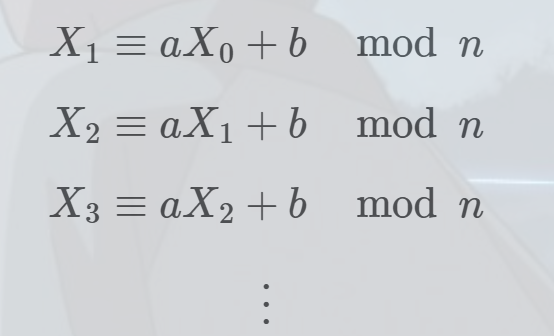Gröbner基学习

发表于 更新于 阅读次数： 本文字数： 10k 阅读时长 ≈ 19 分钟

qaq

大概看了一下，发现自己还是有很多前置知识没解锁，所以暂时先把Gröbner基当做一个求解同余方程组的工具。

Grobner基求的是多元多项式的“最大公约数”。特别地，如果这些多元多项式都有共同的根的话，就可以利用Grobner基来求出这些根。

一般使用sage自带的Ideal.groebner_basis()来求解Grobner基。

举个栗子

1
2
3
4
5
6
7
8
9
10
11
12
13
from Crypto.Util.number import *

p, q = getPrime(256), getPrime(256)
N = p * q
m1 = bytes_to_long(b"flag{12345678901234567890")
m2 = bytes_to_long(b"1234567890123456789012345")
m3 = bytes_to_long(b"6789012345678901234567890}")
e = 17
c1 = pow(m1, e, N)
c2 = pow(m2, e, N)
c3 = pow(m3, e, N)
s = m1 + m2 + m3
print(c1, c2, c3, s)

我们已知模n下的四个多项式

x$^{17}$-c$_1$,y$^{17}$-c$_2$,z$^{17}$-c$_3$,x+y+z-s

直接求即可

1
2
3
4
5
R = PolynomialRing(Zmod(N), 'x, y, z')
x, y, z = R.gens()
I = Ideal([x^e - c1, y^e - c2, z^e - c3, s - x - y - z])
for g in I.groebner_basis():
    print(g)

我们会发现此时的输出为形如

1
2
3
x + 5328981567112615191720220133331441853419574099544130364970268067294655495174350514237016655418948194827654387992772501394750472534171355527604124227050201
y + 5328981567112615191720220133331441853419574099544130364970268067294655495174350514237016655419282307800600127442257417983670074661012643568573635984007124
z + 5328981567112615191720220133331441853419574099544130364970268067294655495174350514237016655332469843107447028137061760530958084317954076142316556455551884

的样子。因为此时我们求解的结果是模n下等于0的，所以取反后模n得到结果

1
2
3
4
5
6
x=-25839761779820419388636354173160318686426155725688192387214644457408201714197935398048859190537833128651541372708198498208898468216133798907945480403976099095196472581975914345018842256150671570416112335389376122987644142545040039609744013377495664352428480978264179709848684985003976793209486651873391260408573227632331918292804048525517538529951150168673237842403628222410136875380676858381038230669925844346174363175099609727392366164076536238932708115735592214234849866166331798535684808968391850739279078686183103096217836987916225524347867439527131715800038836995292599123289863973554898075427671785322409115140
y=-25839761779820419388636354173160318686426155725688192387214644457408201714197935398048859190537833128651541372708198498208898468216133798907945480403976099095196472581975914345018842256150671570416112335389376122987644142545040039609744013377495664352428480978264179709848684985003976793209486651873391260408573227632331918292804048525517538529951150168673237842403628222410136875380676858381038230669925844346174363175099609727392366164076536238932708115735592214234849866166331798535684808968391850739279078686183103096217836987916225524347867439527131715800038836995292599123290104259346020257599917067505049997270
z=-25839761779820419388636354173160318686426155725688192387214644457408201714197935398048859190537833128651541372708198498208898468216133798907945480403976099095196472581975914345018842256150671570416112335389376122987644142545040039609744013377495664352428480978264179709848684985003976793209486651873391260408573227632331918292804048525517538529951150168673237842403628222410136875380676858381038230669925844346174363175099609727392366164076536238932708115735592214234849866166331798535684808968391850739279078686183103096217836987916225524347867439527131715800038836995292599123161209591092660768145554386275785111087
print(long_to_bytes(x%N))
print(long_to_bytes(y%N))
print(long_to_bytes(z%N))

和lcg结合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
flag = b'Spirit{****************************************}'

plaintext = bytes_to_long(flag)
length = plaintext.bit_length()

a = getPrime(length)
b = getPrime(length)
n = getPrime(length)

seed = plaintext
output = []
for i in range(10):
    seed = (a*seed+b)%n
    output.append(seed)

print("output = ",output)
# output =  [9997297986272510947766344959498975323136012075787120721424325775003840341552673589487134830298427997676238039214108, 4943092972488023184271739094993470430272327679424224016751930100362045115374960494124801675393555642497051610643836, 6774612894247319645272578624765063875876643849415903973872536662648051668240882405640569448229188596797636795502471, 9334780454901460926052785252362305555845335155501888087843525321238695716687151256717815518958670595053951084051571, 2615136943375677027346821049033296095071476608523371102901038444464314877549948107134114941301290458464611872942706, 11755491858586722647182265446253701221615594136571038555321378377363341368427070357031882725576677912630050307145062, 7752070270905673490804344757589080653234375679657568428025599872155387643476306575613147681330227562712490805492345, 8402957532602451691327737154745340793606649602871190615837661809359377788072256203797817090151599031273142680590748, 2802440081918604590502596146113670094262600952020687184659605307695151120589816943051322503094363578916773414004662, 5627226318035765837286789021891141596394835871645925685252241680021740265826179768429792645576780380635014113687982]

我们有形如以下的同余方程组

OcWtcU.png

同理就可以用前面的脚本去打

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *

output =  [9997297986272510947766344959498975323136012075787120721424325775003840341552673589487134830298427997676238039214108, 4943092972488023184271739094993470430272327679424224016751930100362045115374960494124801675393555642497051610643836, 6774612894247319645272578624765063875876643849415903973872536662648051668240882405640569448229188596797636795502471, 9334780454901460926052785252362305555845335155501888087843525321238695716687151256717815518958670595053951084051571, 2615136943375677027346821049033296095071476608523371102901038444464314877549948107134114941301290458464611872942706, 11755491858586722647182265446253701221615594136571038555321378377363341368427070357031882725576677912630050307145062, 7752070270905673490804344757589080653234375679657568428025599872155387643476306575613147681330227562712490805492345, 8402957532602451691327737154745340793606649602871190615837661809359377788072256203797817090151599031273142680590748, 2802440081918604590502596146113670094262600952020687184659605307695151120589816943051322503094363578916773414004662, 5627226318035765837286789021891141596394835871645925685252241680021740265826179768429792645576780380635014113687982]

R.<a,b> = PolynomialRing(ZZ)

f1 = output[0]*a + b - output[1]
f2 = output[1]*a + b - output[2]
f3 = output[2]*a + b - output[3]
f4 = output[3]*a + b - output[4]
f5 = output[4]*a + b - output[5]

F = [f1,f2,f3,f4,f5]
# 使用F构建一个理想的Ideal。
ideal = Ideal(F)
# 计算Ideal的Gröbner基I
I = ideal.groebner_basis()
print(I)

#[a + 14335615549654927638941282286970546915595957549605018570782568475122019323510081355298654903631940469827013561488121, b + 4210708565756085546166628092305272946875271265519042415557992126068008771912350261353051723099451508635860890024976, 15756647314623328166703743185062683999338522182906057851774027566229961399311096111735183330556202175961402609739909]

因为此时我们定义的环是ZZ，所以直接使用即可。

我们也可以使用以下代码直接提取得到参数。

1
2
3
a = ZZ(-I[0].univariate_polynomial()(0))
b = ZZ(-I[1].univariate_polynomial()(0))
n = ZZ(I[2])

二元lcg

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from Crypto.Util.number import*
from secret import flag
assert flag[:5] == b'cazy{'
assert flag[-1:] == b'}'
flag = flag[5:-1]
assert(len(flag) == 24)

class my_LCG:
    def __init__(self, seed1 , seed2):
        self.state = [seed1,seed2]
        self.n = getPrime(64)
        while 1:
            self.a = bytes_to_long(flag[:8])
            self.b = bytes_to_long(flag[8:16])
            self.c = bytes_to_long(flag[16:])
            if self.a < self.n and self.b < self.n and self.c < self.n:
                break
    
    def next(self):
        new = (self.a * self.state[-1] + self.b * self.state[-2] + self.c) % self.n
        self.state.append( new )
        return new

def main():
    lcg = my_LCG(getRandomInteger(64),getRandomInteger(64))
    print("data = " + str([lcg.next() for _ in range(5)]))
    print("n = " + str(lcg.n))

if __name__ == "__main__":
    main() 

# data = [2626199569775466793, 8922951687182166500, 454458498974504742, 7289424376539417914, 8673638837300855396]
# n = 10104483468358610819

与上题同理，我们可以列出如下的f

1
2
3
f1 = (a*d[1]+b*d[0]+c-d[2])
f2 = (a*d[2]+b*d[1]+c-d[3])
f3 = (a*d[3]+b*d[2]+c-d[4])

同样用groebner_basis求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
d = [2626199569775466793, 8922951687182166500, 454458498974504742, 7289424376539417914, 8673638837300855396]
n = 10104483468358610819
PR.<a,b,c> = PolynomialRing(Zmod(n))
f1 = (a*d[1]+b*d[0]+c-d[2])
f2 = (a*d[2]+b*d[1]+c-d[3])
f3 = (a*d[3]+b*d[2]+c-d[4])
Fs = [f1, f2, f3]
I = Ideal(Fs)
B = I.groebner_basis()
m = b''
for b in B:
    assert b.degree() == 1
    mi = ZZ(-b(0, 0, 0))
    m += bytes.fromhex(hex(mi)[2:])
print(m)

未知n

这个具体还没咋搞明白为啥groebner基能直接解不带模数的同余方程，自己生成数据检测了一下，感觉需要已知的数据多一点才比较好求。而且也是有概率的。已知的数据越多，成功率越高？这点还不太懂，知道的佬们教教ww

自己先测试一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from Crypto.Util.number import *

flag=b'cazy{L1near_Equ4t1on6_1s_34sy}'
assert flag[:5] == b'cazy{'
assert flag[-1:] == b'}'
flag = flag[5:-1]
assert (len(flag) == 24)


class my_LCG:
    def __init__(self, seed1, seed2):
        self.state = [seed1, seed2]
        self.n = getPrime(64)
        while 1:
            self.a = bytes_to_long(flag[:8])
            self.b = bytes_to_long(flag[8:16])
            self.c = bytes_to_long(flag[16:])
            if self.a < self.n and self.b < self.n and self.c < self.n:
                break

    def next(self):
        new = (self.a * self.state[-1] + self.b * self.state[-2] + self.c) % self.n
        self.state.append(new)
        return new


def main():
    lcg = my_LCG(getRandomInteger(64), getRandomInteger(64))
    print("data = " + str([lcg.next() for _ in range(8)]))
    print("n = " + str(lcg.n))


if __name__ == "__main__":
    main()
    
#data = [2728632062230380206, 12070822170137686159, 4628962860070801596, 5238045249824901416, 11507634387102815130, 10233693222250539355, 3333309580382659734, 3541198295283958454]
#n = 12392832629919082063

在不知道n的情况下用groebner基解一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import*
class my_LCG:
    def __init__(self, seed1, seed2,a,b,c,n):
        self.state = [seed1, seed2]
        self.n = getPrime(64)
        self.a = a
        self.b = b
        self.c = c
    def next(self):
        new = (self.a * self.state[-1] + self.b * self.state[-2] + self.c) % self.n
        self.state.append(new)
        return new

d=[2728632062230380206, 12070822170137686159, 4628962860070801596, 5238045249824901416, 11507634387102815130, 10233693222250539355, 3333309580382659734, 3541198295283958454]
R=PolynomialRing(ZZ,names=['seed1','seed2','a','b','c'])
seed1,seed2,a,b,c=R.gens()
l=my_LCG(seed1,seed2,a,b,c,n)
fs=[l.next()-d[_] for _ in range(8)]
res = Ideal(fs).groebner_basis()
print(res)

#[seed1 + 12289959268929185958, seed2 + 2988362793775166922, a + 6902541827472099082, b + 4217334257707841561, c + 5533442069738943190, 12392832629919082063]

发现是能进行求解的。经过检测发现数据大概在5，6个左右能出的概率就蛮小了。具体原理还是不咋懂，当个黑盒直接用吧XD.

补档:请教了三顺七师傅，有数个方程的根足够小的情况下（比模数小很多），其解极大概率是该格基空间下的最小向量。也就是说当根满足与模数的大小关系时，可以用以上方式求解(大概吧…