GHCTF
ouo
上周天打了GHCTF，题虽然不是特别难(毕竟说的是新生赛)不过也刚好巩固了一下基础
baby_signin
1 | from Crypto.Util.number import getPrime, bytes_to_long |
看到e=4其实就大概有思路了，不是rabin就是e与phi不互素。首先尝试一下二次rabin发现出不来。那么就大致确定是e与phi不互素，最后验证一下发现确实是这样。对于不互素问题我们通常有两种解法。第一种是求gcd(e,phi)=t,把m$^t$看作整体去处理，尝试后发现这个方法在本题中不使用。那么我们就直接进行有限域开根。
1 | from Crypto.Util.number import * |
baby_factor
1 | from Crypto.Util.number import * |
给了phi直接求解就行，没啥好说的。
1 | from Cryptodome.Util.number import * |
EZ_Fermat
1 | from Crypto.Util.number import getPrime, bytes_to_long |
题目给出提示，其实就是考察费马小定理。题目给出了2$^{f(p)}$mod n=w,根据中国剩余定理，很明显对于模p和模q同样成立。同时根据费马小定理2$^{p-1}$=1 mod p，我们可以化简为2$^{f(p)mod(p-1)}$mod p =w那么如何求f(p) mod (p-1)呢。
p≡1mod(p−1)，即 p 除以 p−1的余数为 1。因此，对于任意正整数 k，有：p$^k$≡1$^k$≡1mod (p−1),将 p≡1mod (p−1) 代入 f(p)，得到的正是f(1)的值。即f(p) mod (p-1)=f(1) mod (p-1)再将指数转为f(1),即可得到2$^{f(1)}$mod n=w,即2$^{f(1)}$-w=0 mod n，将1代入多项式求解后取gcd(2$^{f(1)}$-w,n)即可得到p。随后正常求解rsa即可。
1 |
|
baby_factor_revenge
1 | from Crypto.Util.number import * |
一开始以为要根据phi和phi_2的关系分解n之类的，后来发现自己想多了，直接已知phi和n分解n就行，也有现成的板子，也有具体的论文link.springer.com/content/pdf/10.1007/3-540-36492-7_25.pdf
1 | from math import gcd |
baby_lattice
1 | from Crypto.Util.number import * |
从题目代码不难看出是一个LHNP问题。
我们可以据此构造矩阵M。
$$
\left[
\begin{matrix}
p & & & & & \
& p & & \
& &\ddots & & & \
& & & p & & \
-r_1 & -r_2 &\cdots &-r_n & k/p \
c_1 & c_2 & \cdots & c_n& &k \
\end{matrix}
\right]
$$
满足以下等式
（k$_1$,k$_2$,……k$_t$,x,1)M=(e$_1$,e$_2$,…..e$_t$,kx/p,k),LLL求解即可。
1 | from Crypto.Cipher import AES |
RSA_and_DSA
1 | from random import getrandbits, randint |
不难看出是一个RSA和DSA的拼接，前半部分是一个RSA的维纳攻击，用正常连分数展开去打就可以，后半部分是一个DSA签名的线性K问题，具体的推导过程可以参考另一篇博客DSA签名 | 浮白载笔，这里就不过多赘述。
1 | from Cryptodome.Cipher import AES |
MIMT_RSA
1 | from Crypto.Util.number import * |
一个很基本的RSA加密系统，并且给出了
1 | assert int(KEY).bit_length() == 36 |
说明key的大小不大，结合题目MIMT(其实应该是MITM)也就是中间相遇攻击，说明爆破是可行的。并且KEY并不是一个素数，所以我们可以通过爆破其因子来间接得到KEY.
稍微推导一下
KEY$^e$≡ck(mod n)
(a∗b)$^e$≡ck (modn)
b$^e$≡ck*a$^{−e}$(modn)
所以分别爆破a和b即可。
1 | from tqdm import trange |
EZ_Fermat_bag_PRO
1 | from Crypto.Util.number import getPrime, bytes_to_long |
这次的多项式中既有p也有q，所以我们要想办法消去一个。只要给原版的多项式乘上p$^{32}$，就可以消掉全部的q.
消去后的多项式如下。
1 | n**31*p + 2*n**30*p**3 - n**30*p**2 - n**29*p**3 + n**28*p**7 - 2*n**28*p**6 + 2*n**28*p**5 - n**28*p**4 + 6*n**27*p**9 - 2*n**27*p**8 - n**27*p**7 - n**27*p**6 - 2*n**27*p**5 - n**26*p**10 - 5*n**26*p**9 + n**26*p**8 + 2*n**26*p**7 - 3*n**26*p**6 + n**25*p**13 + n**25*p**12 + n**25*p**10 + 2*n**25*p**9 - 3*n**25*p**8 - 2*n**25*p**7 + 5*n**24*p**15 + 3*n**24*p**13 - n**24*p**12 + 4*n**24*p**11 + n**24*p**10 + 5*n**24*p**9 - n**24*p**8 + n**23*p**16 - 2*n**23*p**15 + n**23*p**14 + 3*n**23*p**12 - 5*n**23*p**10 - 4*n**23*p**9 - 3*n**22*p**19 + 2*n**22*p**18 - 5*n**22*p**17 - n**22*p**16 + n**22*p**15 + n**22*p**13 + 2*n**22*p**12 - n**22*p**11 + 3*n**22*p**10 + n**21*p**20 - 2*n**21*p**19 - 2*n**21*p**18 - 2*n**21*p**17 - n**21*p**16 + n**21*p**15 - n**21*p**13 + 2*n**21*p**12 - 2*n**21*p**11 - 2*n**20*p**23 - n**20*p**22 - n**20*p**21 + n**20*p**20 - 2*n**20*p**18 - n**20*p**17 + n**20*p**16 - 5*n**20*p**15 + 2*n**20*p**14 - 2*n**20*p**13 + n**19*p**25 - 3*n**19*p**24 - 2*n**19*p**22 - n**19*p**19 + 4*n**19*p**18 + n**19*p**16 - 3*n**19*p**15 + 3*n**19*p**14 + 2*n**19*p**13 + n**18*p**27 - 2*n**18*p**26 + 5*n**18*p**25 + n**18*p**24 - 4*n**18*p**23 - 2*n**18*p**20 - 4*n**18*p**19 - n**18*p**16 + n**17*p**29 + n**17*p**27 - 2*n**17*p**26 + 2*n**17*p**25 - n**17*p**23 - 2*n**17*p**22 - 2*n**17*p**21 + n**17*p**19 + n**17*p**18 + n**17*p**17 - 2*n**17*p**16 - n**16*p**31 - n**16*p**30 + n**16*p**29 + 2*n**16*p**28 + 3*n**16*p**27 - n**16*p**26 - n**16*p**25 - n**16*p**24 + 2*n**16*p**23 + 2*n**16*p**22 + n**16*p**21 + 4*n**16*p**20 + 2*n**16*p**18 + n**16*p**17 - 4*n**15*p**33 + n**15*p**32 + n**15*p**31 + n**15*p**30 + n**15*p**29 + 4*n**15*p**28 + 2*n**15*p**26 - n**15*p**25 - n**15*p**24 + n**15*p**23 + 2*n**15*p**22 - 4*n**15*p**21 + 2*n**15*p**20 - 3*n**15*p**19 - 3*n**15*p**18 - 5*n**14*p**35 + n**14*p**33 - 2*n**14*p**32 - n**14*p**31 - n**14*p**30 - 2*n**14*p**29 + 4*n**14*p**28 - 2*n**14*p**27 + 3*n**14*p**23 - n**14*p**22 + n**14*p**20 + 3*n**14*p**18 + n**13*p**37 + n**13*p**35 - 3*n**13*p**34 - 4*n**13*p**33 + 2*n**13*p**32 + 2*n**13*p**31 - 2*n**13*p**29 - n**13*p**28 + n**13*p**26 - n**13*p**25 + n**13*p**23 + 2*n**13*p**22 - 4*n**13*p**20 - 3*n**13*p**19 - 4*n**12*p**39 + 2*n**12*p**38 - n**12*p**36 - 3*n**12*p**35 - n**12*p**34 - n**12*p**33 - n**12*p**32 + 2*n**12*p**31 + 2*n**12*p**30 + n**12*p**28 - n**12*p**27 + n**12*p**26 - n**12*p**25 + 4*n**12*p**24 + n**12*p**23 - n**12*p**22 - 2*n**12*p**21 - 2*n**12*p**20 - n**11*p**41 - 4*n**11*p**40 + 2*n**11*p**39 + 4*n**11*p**38 + n**11*p**37 + 2*n**11*p**36 - 2*n**11*p**35 - n**11*p**34 + 3*n**11*p**33 + 3*n**11*p**32 + n**11*p**31 + 6*n**11*p**30 + 2*n**11*p**27 + 2*n**11*p**26 - 2*n**11*p**25 + 2*n**11*p**24 - n**11*p**23 - 3*n**11*p**22 + 3*n**11*p**21 - 3*n**10*p**42 + 2*n**10*p**41 - 5*n**10*p**39 - n**10*p**37 - n**10*p**36 - 3*n**10*p**35 + 2*n**10*p**34 - 2*n**10*p**33 + n**10*p**32 + 3*n**10*p**31 + 3*n**10*p**30 + 2*n**10*p**29 + 3*n**10*p**28 + 4*n**10*p**27 + n**10*p**26 - 3*n**10*p**25 - n**10*p**24 + 2*n**10*p**23 - n**9*p**43 - 3*n**9*p**42 + 2*n**9*p**41 - n**9*p**40 + 2*n**9*p**39 - 4*n**9*p**38 + n**9*p**37 + 4*n**9*p**36 - 5*n**9*p**35 - 2*n**9*p**34 + n**9*p**33 + 3*n**9*p**32 - 5*n**9*p**31 + 3*n**9*p**30 + 3*n**9*p**28 + 4*n**9*p**27 - 4*n**9*p**26 - 4*n**9*p**25 - n**9*p**24 + 4*n**9*p**23 + 3*n**8*p**47 - 3*n**8*p**46 - 3*n**8*p**44 - 5*n**8*p**43 + n**8*p**42 + n**8*p**41 + 2*n**8*p**40 - 5*n**8*p**39 - n**8*p**36 + 2*n**8*p**35 - n**8*p**33 + 5*n**8*p**32 - n**8*p**31 + n**8*p**30 + 3*n**8*p**29 + 2*n**8*p**27 - 2*n**8*p**26 + n**8*p**25 - 2*n**8*p**24 - 4*n**7*p**49 - 3*n**7*p**48 - n**7*p**47 - 2*n**7*p**45 - 3*n**7*p**44 - n**7*p**42 - n**7*p**40 + n**7*p**39 + 2*n**7*p**38 + 2*n**7*p**36 - 3*n**7*p**35 + 2*n**7*p**33 - 2*n**7*p**32 - 4*n**7*p**31 - n**7*p**30 + n**7*p**29 - 2*n**7*p**27 + 2*n**7*p**26 - 2*n**6*p**50 + n**6*p**49 - 2*n**6*p**48 - 2*n**6*p**47 + n**6*p**46 + n**6*p**44 - n**6*p**43 - n**6*p**42 - n**6*p**41 + 4*n**6*p**40 - n**6*p**39 - 2*n**6*p**38 - 2*n**6*p**37 - n**6*p**36 - n**6*p**35 - 3*n**6*p**34 + 5*n**6*p**33 - n**6*p**32 + 3*n**6*p**31 + 3*n**6*p**30 - 2*n**6*p**29 + 4*n**6*p**28 - n**6*p**27 - 3*n**6*p**26 - n**5*p**52 - 2*n**5*p**51 - n**5*p**50 - 3*n**5*p**49 - n**5*p**46 - n**5*p**45 - 3*n**5*p**44 - n**5*p**43 - 3*n**5*p**42 + 3*n**5*p**41 - 2*n**5*p**40 + n**5*p**39 + 2*n**5*p**38 + n**5*p**37 - n**5*p**36 - n**5*p**35 + n**5*p**32 - n**5*p**31 + 3*n**5*p**30 + 3*n**5*p**29 - 2*n**5*p**28 + 2*n**4*p**55 - n**4*p**54 - n**4*p**53 + 2*n**4*p**52 + n**4*p**51 + 5*n**4*p**50 - n**4*p**49 + 2*n**4*p**45 + 2*n**4*p**44 - 2*n**4*p**42 - n**4*p**41 - n**4*p**40 - 3*n**4*p**39 - 5*n**4*p**38 - n**4*p**37 + n**4*p**36 - n**4*p**34 + n**4*p**33 - 4*n**4*p**32 + 2*n**4*p**30 - 2*n**4*p**29 - 2*n**4*p**28 + 7*n**3*p**57 + 2*n**3*p**56 + 3*n**3*p**55 + n**3*p**54 - 2*n**3*p**53 + n**3*p**52 - n**3*p**50 - n**3*p**49 - 2*n**3*p**48 - 2*n**3*p**46 + 2*n**3*p**45 + 2*n**3*p**43 - n**3*p**42 - n**3*p**41 + n**3*p**40 + n**3*p**38 + n**3*p**37 - 2*n**3*p**36 - 3*n**3*p**35 - 2*n**3*p**34 + 6*n**3*p**32 + n**3*p**31 - 3*n**3*p**30 + 3*n**3*p**29 - 2*n**2*p**59 + 2*n**2*p**58 - 2*n**2*p**56 + n**2*p**54 - 2*n**2*p**53 + n**2*p**52 + 2*n**2*p**51 - 2*n**2*p**50 - n**2*p**49 - n**2*p**47 - n**2*p**46 - 2*n**2*p**45 - 3*n**2*p**44 + n**2*p**43 + 2*n**2*p**42 - 2*n**2*p**41 + n**2*p**40 + 5*n**2*p**39 + 3*n**2*p**35 + n**2*p**33 + 6*n**2*p**32 - 2*n**2*p**31 + n**2*p**30 - n*p**61 - 3*n*p**60 - n*p**59 + 3*n*p**58 + n*p**57 + n*p**56 + 2*n*p**54 - n*p**53 + 2*n*p**52 - n*p**51 + 2*n*p**50 - 4*n*p**47 + n*p**46 + 3*n*p**45 + n*p**44 + n*p**43 + n*p**42 + n*p**41 - 2*n*p**40 - 3*n*p**39 - n*p**38 - 3*n*p**35 - 2*n*p**34 - 2*n*p**33 - n*p**32 + 2*n*p**31 + p**63 - 2*p**62 - 2*p**61 + 3*p**60 + p**59 + 3*p**57 - p**56 + p**55 - p**54 - 3*p**53 + p**52 - p**50 - p**49 - 3*p**48 - p**47 - p**46 + 3*p**44 - p**42 + 4*p**41 + 2*p**40 + 2*p**39 - 4*p**38 + p**37 + 2*p**36 - 5*p**35 + 2*p**34 - 2*p**33 - 2*p**32 |
但这里的推导与EZ_Fermat有所不同。消去q后，我们有2$^{f(p)*p^{32}}$$\equiv$w$^{p^{32}}$mod(n),由费马小定理可以推得2$^{f(p)p^{32}}$$\equiv$w mod(p).需要将指数换元为（x-1）的形式才能应用费马小定理进行化简。比如2$^{pn^{32}}$化为2$^{(p-1)n^{32}}$此时等式右边就要乘一个2$^{-1n^{32}}$，以此类推即可。
1 | N = 95656952327201449381426394713246214670537600365883923624876350719801926817916514429721785287844335184715049179879891389941974481490433975689601829920289485889138252888029716516069912637121531561601839948367426922036690701168975937162280451323099126372019216020898338909808577022618554997063496690156977790629 |
多嘴解释几句
**zip(f.monomials(), f.coefficients())**：
- **
f.monomials()**：这个方法返回多项式f的所有单项式（monomials）。例如，如果 ( f(n, p) = 2n^2p + 3np^2 + 5 )，f.monomials()返回[n^2*p, n*p^2, 1]。 - **
f.coefficients()**：这个方法返回与多项式中每一个单项式对应的系数。例如，对应于上述多项式，f.coefficients()可能返回[2, 3, 5]。 - **
zip(...)**：这两个列表会被结合，形成一个迭代器。如此一来，我们在遍历时能同时得到单项式i和其系数j，例如：1
[(n^2*p, 2), (n*p^2, 3), (1, 5)]
- **
1 |
|
那么对于本题来说，c≡256$^{81}$$$pre+256$$m+suf (mod p）,其中pre指‘NSSCTF{’，suf指‘}’。我们中间填充b’0‘那么就可得到m≡(c−256$^{81}$$*$pre−b’0’*80-suf)(mod p),
有了这点就可以造格了。(懒得latex了，手写一下)
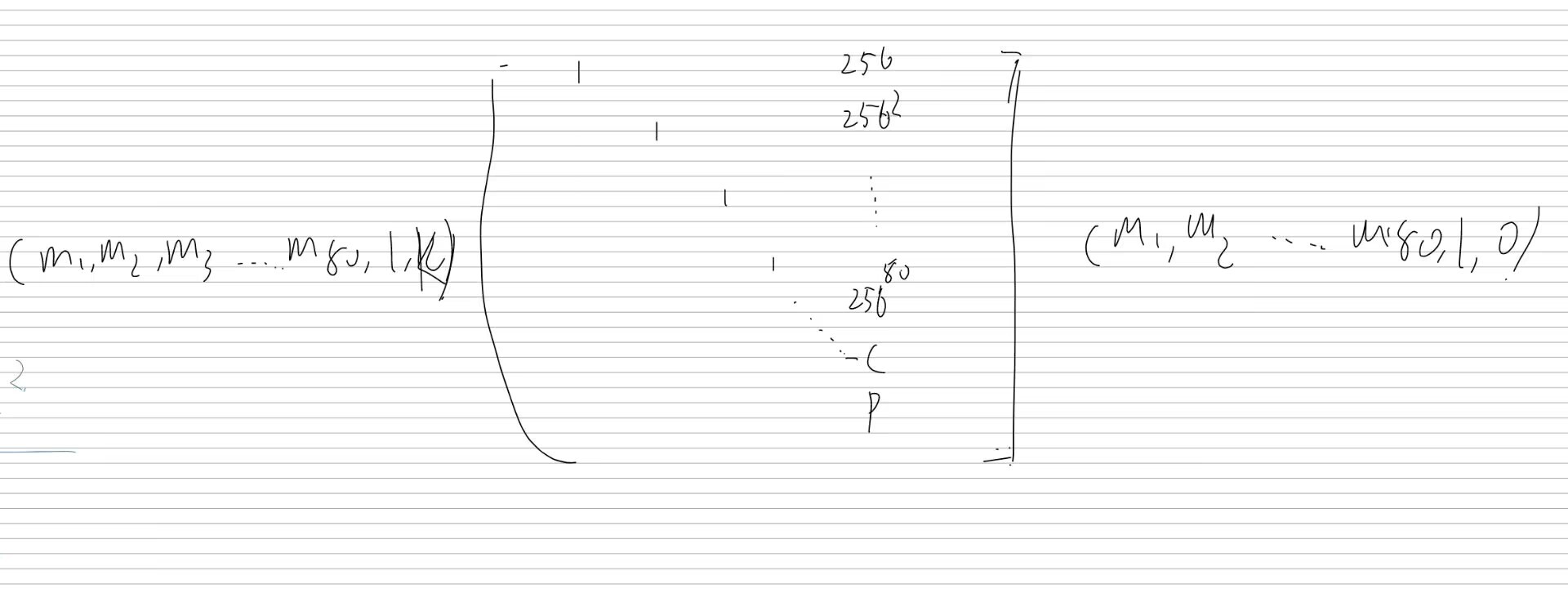
加强了解的话可以去做一下鸡块师傅的ezmod系列。2024-NSSCTF-密码工坊非官方dlc-wp-crypto | 糖醋小鸡块的blog
1 | from Crypto.Util.number import * |